Introduction
“Feature engineering” refers to the process of modifying features (variables or columns) to provide machine learning models with data they can interpret and manage effectively. These modifications may involve altering a single feature, applying mathematical transformations, or creating new features from existing ones. As one of the most crucial processes in machine learning, feature engineering often determines whether a model performs well or poorly.
For those who approach machine learning with a statistical background, clarification is necessary before diving into the complex field of Feature Engineering.
This is simply a matter of terminology but can lead to significant confusion if left unexplained.
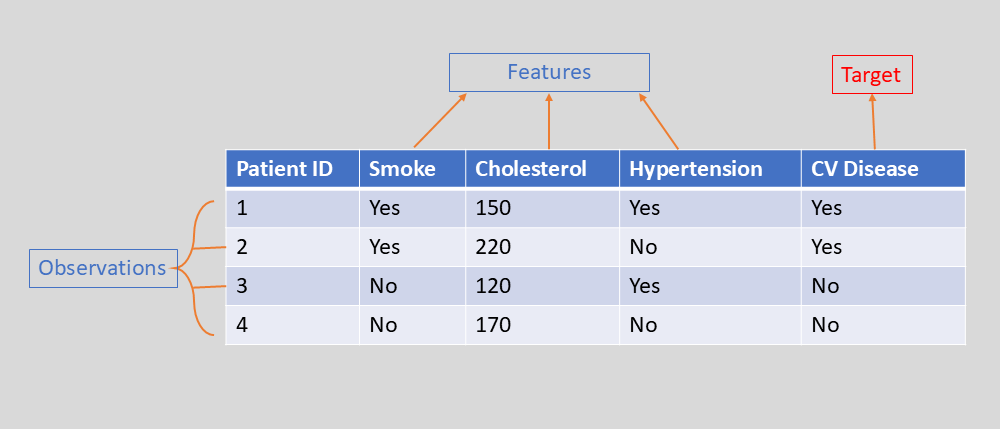
In Machine Learning, we use the terms “Features” and “Target” to refer to what statisticians typically call “Independent Variables” and “Dependent Variables,” respectively.
The variables under study are arranged in columns in a dataset with tabular organization. Some of these columns are used as “independent variables” or “features,” while one usually serves as the objective of our analysis—the “Dependent Variable” or “target.”
The observations (number of cases, etc.) are arranged along the rows.
Feature Modification
Feature modification involves altering a variable’s content to enhance its comprehensibility or make it more manageable for the model. This process typically employs mathematical or statistical manipulation techniques.
Normalization and standardization: These transformations, discussed elsewhere, reduce the influence of extreme values. They’re essential for scale-sensitive models like regression.
Logarithmic transformation or power elevation: These are beneficial for asymmetrically distributed data. They can help achieve a more normal-like distribution.
Removal or reduction of outliers.
Binning: This technique divides a continuous variable into discrete groups. It’s useful for preserving information in variables with non-linear distributions.
Creating New Features
The creation of new features aims to extract valuable information by combining existing features in various ways.
Combinatory features: Derived by applying mathematical operations (addition, multiplication, division) to existing features in the dataset.
Temporal features: Capture information from time-based data, such as day, month, or season, to incorporate temporal aspects into the analysis.
Encoding: Transforms categorical variables into numerical values (to be discussed in detail elsewhere).
Polynomial features: Extract complex relationships from existing variables using polynomial terms.
Let’s now explore an example of feature engineering, applying various techniques to a generic dataset.
To do this, let’s imagine a dataset containing temporal information, recording date, rainfall, temperatures and sales. We’ll create it using pandas.
import pandas as pd
# Creating a sample dataset
data = {
'Date': ['2024-01-01', '2024-01-02', '2024-01-03', '2024-01-04', '2024-01-05'],
'Temperature': [15, 14, 15, 13, 16],
'Rainfall': [0.0, 0.2, 0.0, 0.5, 0.1],
'Sales': [200, 210, 190, 205, 198]
}
df = pd.DataFrame(data)
df['Date'] = pd.to_datetime(df['Date'])
print(df)Let’s add temporal features by extracting them from the “date” feature:
# Add the day of the week
df['Day_of_Week'] = df['Date'].dt.dayofweek # Monday=0, Sunday=6
# Add the month
df['Month'] = df['Date'].dt.month
# Display the dataset with the new features
print(df)Let’s create a new feature that combines those containing rainfall and temperature data.
# Creating a combinatory feature
df['Temp_Rain_Interaction'] = df['Temperature'] * df['Rainfall']
print(df[['Temperature', 'Rainfall', 'Temp_Rain_Interaction']])We can transform Sales into logarithmic format, in case it doesn’t have a normal distribution.
import numpy as np
# Logarithmic transformation of the Sales variable
df['Log_Sales'] = np.log(df['Sales'])
print(df[['Sales', 'Log_Sales']])We can apply the Binning technique to the temperature variable
# Defining temperature bins
bins = [0, 10, 15, 20]
labels = ['Low', 'Medium', 'High']
df['Temp_Binned'] = pd.cut(df['Temperature'], bins=bins, labels=labels)
print(df[['Temperature', 'Temp_Binned']])Let’s standardize or normalize some variables
# Normalization of the Sales variable (brought to range [0, 1])
df['Sales_Normalized'] = (df['Sales'] - df['Sales'].min()) / (df['Sales'].max() - df['Sales'].min())
# Standardization of the Temperature variable (brought to mean 0 and standard deviation 1)
df['Temperature_Standardized'] = (df['Temperature'] - df['Temperature'].mean()) / df['Temperature'].std()
print(df[['Sales', 'Sales_Normalized', 'Temperature', 'Temperature_Standardized']])Feature Selection
Feature selection techniques aim to retain only the most relevant features for the model we’re building while removing less significant ones. This process is crucial as it enhances model performance, mitigates overfitting risk, and reduces computation time.
Unlike dimensionality reduction techniques, which we’ll explore later, feature selection preserves the original features, simply “choosing” the most impactful ones. Both approaches share the goal of feature reduction, but dimensionality reduction goes further by radically transforming the original features. This creates more compact—though less interpretable—new features.
There are three main Feature Selection methods: filtering, wrapper, and embedded.
Filtering Methods
These methods evaluate features using statistical techniques, independent of the specific Machine Learning application. As a result, they are faster and less computationally intensive.
Correlation: Calculates the correlation between features and the target variable. Features with low correlation are eliminated.
Chi-square: Used for categorical variables. If a feature is found to be independent of the target variable through this test, it’s considered less important.
ANOVA (Analysis of Variance): An ANOVA test determines which features significantly impact the target variable.
Mutual Information: Measures the dependence between features and the target variable. Features with high mutual information are retained.
Wrapper Methods
Wrapper methods develop Machine Learning models using various feature sets, selecting combinations that yield optimal model performance. These methods are more time-consuming and computationally expensive, as the model must be retrained for each feature set combination.
Recursive Feature Elimination (RFE): The model is initially trained with all features, then the least important ones are removed one by one until reaching the desired feature set size.
Forward Selection: Starting with a model without features, this method gradually adds features one at a time, selecting the one that most improves performance at each step.
Backward Elimination: Beginning with a model containing all features, this approach progressively removes the least influential ones. Unlike RFE, which evaluates feature elimination based on model characteristics, Backward Elimination uses statistical criteria for selection.
Embedded Methods
Embedded methods are integrated into the model’s algorithm. They assess which features to eliminate directly during model training. These methods require only a single model training and are more efficient—both computationally and time-wise—compared to wrapper methods.
Lasso Regression (Least Absolute Shrinkage and Selection Operator): A regression model that shrinks the coefficients of less influential features toward zero, effectively eliminating them.
Decision Trees and Random Forest: Algorithms that inherently perform feature selection by discarding less important features in their various tree structures.
Support Vector Machine (SVM): Can apply a penalty to features with low coefficients, aiding in feature selection.
Feature Engineering for Medical Data
Real-world medical datasets often contain redundant or incomplete information, noise, missing data, and are frequently difficult to identify.
Feature Engineering techniques therefore represent an extremely important moment for their analysis.
In summary, the most frequently applied techniques concern
- The management of missing values
- the encoding of categorical data (see section Encoding of Categorical Data)
- standardization and normalization
- creation of new variables (risk scores or clinical indices)
- management of outliers
By applying feature engineering techniques when necessary, it is possible to transform poorly predictive models into high-performing and clinically useful models.
Feature Engineering in Python: A Practical Example
In the following example, we’ll create a dataset of fictitious medical data and apply various Feature Selection techniques using Python.
Importing librarias:
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression, LassoCV
from sklearn.feature_selection import RFE, SelectKBest, chi2, f_classif, mutual_info_classif
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
Generate a syntetic dataset:
np.random.seed(42)
data = {
'age': np.random.randint(20, 80, 100),
'bmi': np.random.normal(25, 5, 100),
'blood_pressure': np.random.normal(120, 15, 100),
'cholesterol': np.random.normal(200, 25, 100),
'glucose': np.random.normal(100, 20, 100),
'smoking': np.random.randint(0, 2, 100),
'exercise': np.random.randint(0, 2, 100),
'disease_risk': np.random.randint(0, 2, 100) # target variable
}
df = pd.DataFrame(data)Separate features from the target variable and create standardized features (essential for certain algorithms like Lasso)
X = df.drop('disease_risk', axis=1)
y = df['disease_risk']
# Standardize features
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)Application of filtering methods:
### Filter Methods ###
# Correlation threshold (e.g., remove features with low correlation to target)
correlation_threshold = 0.1
correlations = X.corrwith(y)
selected_features_corr = correlations[abs(correlations) > correlation_threshold].index.tolist()
print("Filter method (correlation) selected features:", selected_features_corr)
# ANOVA F-test for continuous features
f_test = SelectKBest(score_func=f_classif, k=5)
f_test.fit(X, y)
selected_features_anova = X.columns[f_test.get_support()].tolist()
print("Filter method (ANOVA F-test) selected features:", selected_features_anova)
# Chi-squared test for categorical data (need integer features for chi-squared test)
chi2_test = SelectKBest(score_func=chi2, k=5)
X_int = X[['age', 'smoking', 'exercise']] # only integer features
chi2_test.fit(X_int, y)
selected_features_chi2 = X_int.columns[chi2_test.get_support()].tolist()
print("Filter method (Chi-squared test) selected features:", selected_features_chi2)
# Mutual Information
mi_test = SelectKBest(score_func=mutual_info_classif, k=5)
mi_test.fit(X, y)
selected_features_mi = X.columns[mi_test.get_support()].tolist()
print("Filter method (Mutual Information) selected features:", selected_features_mi)Application of wrapper method (RFE)
### Wrapper Methods (Recursive Feature Elimination) ###
# RFE with Logistic Regression
model = LogisticRegression(max_iter=1000)
rfe_selector = RFE(estimator=model, n_features_to_select=3)
rfe_selector = rfe_selector.fit(X_scaled, y)
selected_features_rfe = X.columns[rfe_selector.support_].tolist()
print("Wrapper method (RFE) selected features:", selected_features_rfe)
Application of embedded methods
### Embedded Methods ###
# Lasso Regression (L1 Regularization)
lasso = LassoCV(cv=5)
lasso.fit(X_scaled, y)
selected_features_lasso = X.columns[(lasso.coef_ != 0)].tolist()
print("Embedded method (Lasso) selected features:", selected_features_lasso)
# Feature importance with Random Forest
rf = RandomForestClassifier(n_estimators=100, random_state=42)
rf.fit(X, y)
importances = rf.feature_importances_
selected_features_rf = X.columns[np.argsort(importances)[-3:]].tolist() # Select top 3 features
print("Embedded method (Random Forest) selected features:", selected_features_rf)Features selected by various methods:
| Filter | Features selected |
| Correlation | [‘age’, ‘blood_pressure’, ‘smoking’, ‘exercise’] |
| ANOVA F-test | [‘age’, ‘blood_pressure’, ‘glucose’, ‘smoking’, ‘exercise’] |
| Chi-squared | [‘age’, ‘smoking’, ‘exercise’] |
| Mutual Information | [‘blood_pressure’, ‘cholesterol’, ‘glucose’, ‘smoking’, ‘exercise’] |
| RFE | [‘age’, ‘blood_pressure’, ‘smoking’] |
| Lasso | [] |
| Random Forest | [‘cholesterol’, ‘glucose’, ‘blood_pressure’] |
As can be observed from the results presented above, the various feature selection methods do not yield identical outcomes. While there is often consensus on certain features across multiple techniques, significant differences can emerge in the final selection. This variability highlights the importance of carefully considering the choice of feature selection method, as it can substantially impact which features are ultimately retained for model development. The discrepancies between methods underscore the complexity of feature selection and suggest that relying on a single approach may not always provide the most comprehensive or accurate representation of feature importance. Therefore, data scientists and machine learning practitioners should carefully evaluate and potentially combine multiple feature selection techniques to ensure a robust and well-informed feature set for their specific problem domain and modeling objectives.
Conclusion
Feature engineering and selection are crucial phases in the machine learning process—fundamental to the success of predictive models. These techniques span from simple variable modifications to new feature creation and sophisticated selection methods. A balanced, combined approach that considers the specific application domain and model objectives is often necessary. Effective feature engineering and selection improve model performance while reducing overfitting risk and computation times, making them essential elements of any successful machine learning project.


