Overview and Methodology
Monte Carlo simulation is a statistical tool used for problems with uncertain solutions, particularly those involving multiple variables with unknown values.
It runs multiple simulations of the problem, generating random values for the relevant variables each time.
The method takes its name from Monte Carlo, a city famous for its gambling and games of chance, reflecting how the simulation uses randomly generated variables.
At its core, Monte Carlo simulation relies on variables that have unknown values but follow known distributions. The method generates random values for these variables thousands or millions of times. This process yields important statistical metrics—like means and distributions—which form the basis for the final results.
Beyond the variables themselves, the simulation requires a model that connects these variables to the outcome.
Applications in Medicine
- Risk Prediction: Monte Carlo methods help predict event risks in oncology and other medical fields by analyzing multiple variables.
- Treatment Outcome Assessment: The simulation predicts treatment outcomes effectively, even when working with uncertain clinical data.
- Healthcare Policy Evaluation: Monte Carlo simulations assess the potential outcomes of mass screening programs and healthcare policy initiatives.
- Resource Management: The method helps evaluate and predict patient loads across hospitals, departments, and individual wards.
Operating Procedures
To perform a Monte Carlo evaluation, you need to:
- Analyze the variables involved in the phenomenon or process under study. In medicine, these typically include age, sex, weight, and—depending on the research focus—clinical data and therapeutic indicators.
- Determine the statistical distribution for each chosen variable. These may be normal or Gaussian for continuous variables (like age or blood pressure), binomial for two-value variables (sick/healthy, pathological/normal, alive/dead), or Poisson for repeated binomial variables.
- Establish the model that connects variables to outcomes. This can be done empirically (through statistical analysis of available data), theoretically (such as using pharmacokinetic laws for drug studies), or through a mixed approach combining both empirical and theoretical data.
With this information in hand, we can implement the Monte Carlo simulation. Based on the variables’ distribution characteristics and our model, the simulation runs thousands of iterations using random data values and tracks their effect on outcomes. The analysis of these numerous iterations produces a results distribution that informs decision-making.
Problems and Limitations
To perform a Monte Carlo simulation, three key elements are essential: identified variables, known distributions for those variables, and a model that connects them to the desired outcome or process.
A significant challenge arises when variable distributions are unclear, particularly with limited available data.
Model development presents another hurdle—a model that’s too simplified may not reflect reality, while an overly complex one becomes difficult to implement and validate.
In medical applications, particularly for risk assessment, statistical regression typically forms the foundation of the model.
The process involves incorporating observational or experimental clinical study data into a regression model—whether linear, logistic, or Cox for survival data—to link variables to outcomes. These models provide valuable accuracy metrics (r-squared, AUC, Log-rank, etc.) before their integration into the Monte Carlo simulation.
Practical Benefits
Monte Carlo simulation extends beyond traditional statistical models derived from observational or experimental clinical studies. While conventional linear or logistic regression models estimate outcomes based on mean values from initial data, Monte Carlo offers more.
The simulation generates random values across the full range of input data, revealing how outcomes change with varying conditions. This approach provides a comprehensive view of possible outcomes based on mean values and across the entire distribution of independent variables. As a result, we can generate detailed risk distribution curves.
This capability allows us to explore multiple scenarios, such as comparing outcomes for patients with high, medium, or low input values, and identifying critical risk thresholds.enabling users to analyze real data with ease while providing flexibility, computational efficiency, and seamless integration with Python’s scientific ecosystem.
Monte Carlo Simulation in Python
Python offers several standard libraries for implementing Monte Carlo simulations, including NumPy, SciPy, Pandas, and Matplotlib.
The NumPy library’s powerful random number generation capabilities provide everything needed to simulate events with specific distributions in defined ranges.
For example, to simulate an age distribution from 20 to 80 years with a uniform distribution, you can use this simple code:
ages = np.random.uniform(20, 80, num_patients)
Or to simulate a binary variable, such as whether a treatment is applied:
treatment = np.random.choice([0, 1], size=num_patients)
For more complex Monte Carlo simulations, specialized libraries are available: PyMC3 for Bayesian statistics and TensorFlow Probability for stochastic simulations.
Example 1: Survival Simulation with Monte Carlo Simulation
Consider a scenario with a patient’s annual survival rate of 85% (p=0.85).
The model has two key parameters: the total number of patients (n) and the annual survival probability (p).
Events follow a binomial distribution based on n and p:
![]()
For cumulative survival, patients who survive at year’s end become the exposed population for the following year:
![]()
This model is admittedly simplistic. It assumes both patient independence and a constant annual survival rate across all patients and years—assumptions that don’t reflect reality.
However, it serves well to demonstrate Monte Carlo simulation.
Below is the commented Python code:
Required Python Libraries:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
Step 1: define the simulation parameters
np.random.seed(42) # Setting seed for reproducibility
num_patients = 1000 # Number of patients in the study
num_simulations = 1000 # Number of Monte Carlo iterations
survival_probability_yearly = 0.85 # Probability of survival each year
num_years = 5 # Total number of years to simulate
Step 2: create an array to store results of each simulation and runs the simulation
survival_data = np.zeros((num_simulations, num_years))
for sim in range(num_simulations):
# Start with all patients alive
survivors = num_patients
for year in range(num_years):
# Simulate survival for the current year based on survivors from the previous year
survivors = np.random.binomial(survivors, survival_probability_yearly)
survival_data[sim, year] = survivors / num_patients * 100 # Store survival as percentag
Step 3: calculate metrics
mean_survival = survival_data.mean(axis=0)
std_survival = survival_data.std(axis=0)
Step 4: visualize results
plt.figure(figsize=(10, 6))
years = np.arange(1, num_years + 1)
plt.errorbar(years, mean_survival, yerr=std_survival, fmt='-o', capsize=5, label='Mean Survival ± Std Dev')
plt.title('Monte Carlo Simulation of Survival Over Time')
plt.xlabel('Year')
plt.ylabel('Survival Rate (%)')
plt.xticks(years)
plt.grid(True)
plt.legend()
plt.show()
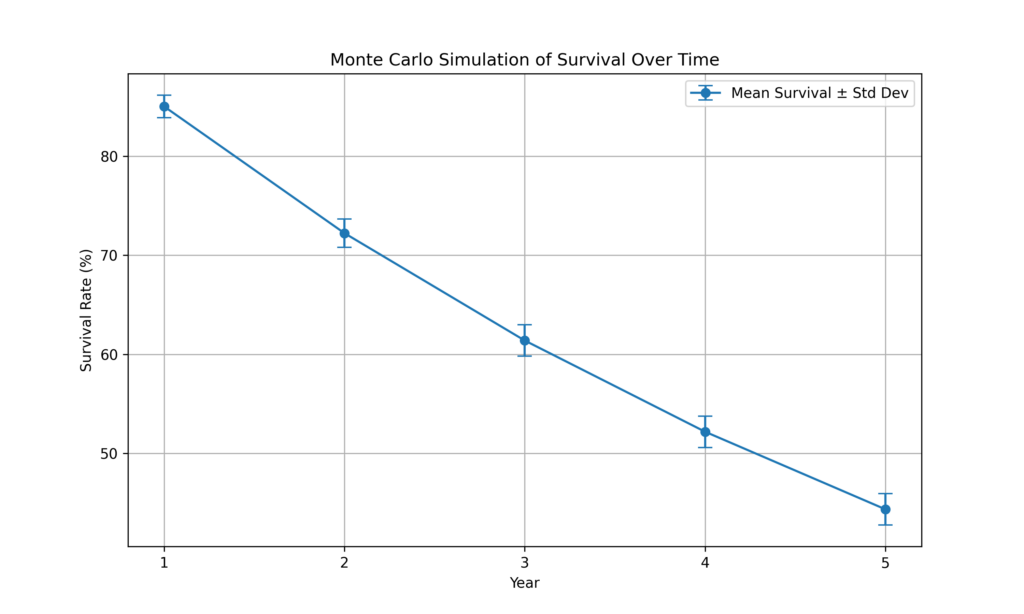
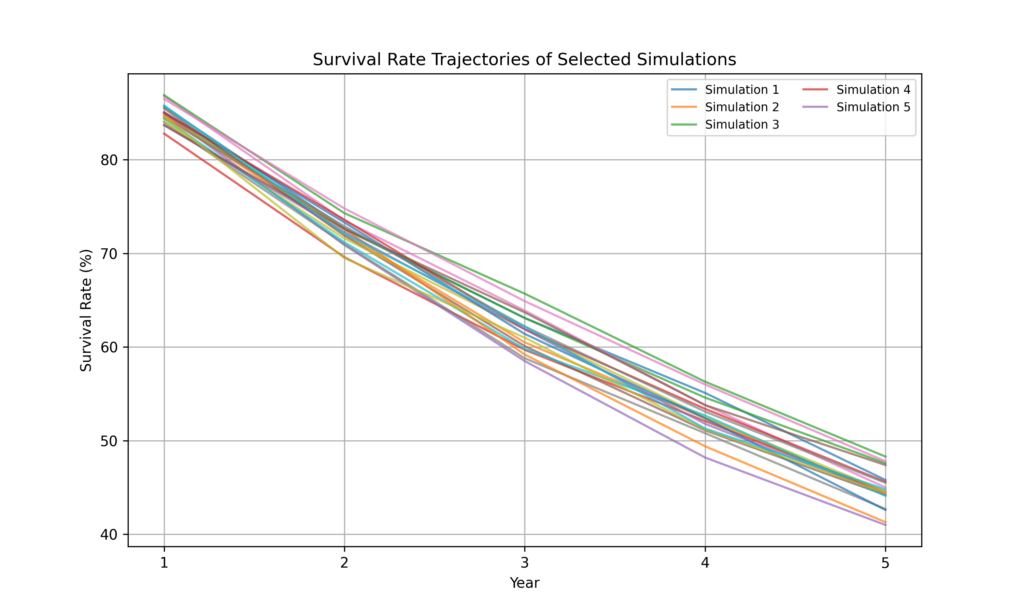
Step 4: visualize survival trajectories of a subset of simulations
plt.figure(figsize=(10, 6))
for i in range(20): # Plot trajectories for 20 random simulations
plt.plot(years, survival_data[i, :], alpha=0.7, label=f'Simulation {i+1}' if i < 5 else "")
plt.title('Survival Rate Trajectories of Selected Simulations')
plt.xlabel('Year')
plt.ylabel('Survival Rate (%)')
plt.xticks(years)
plt.grid(True)
plt.legend(loc='upper right', fontsize='small', ncol=2, frameon=True)
plt.show()
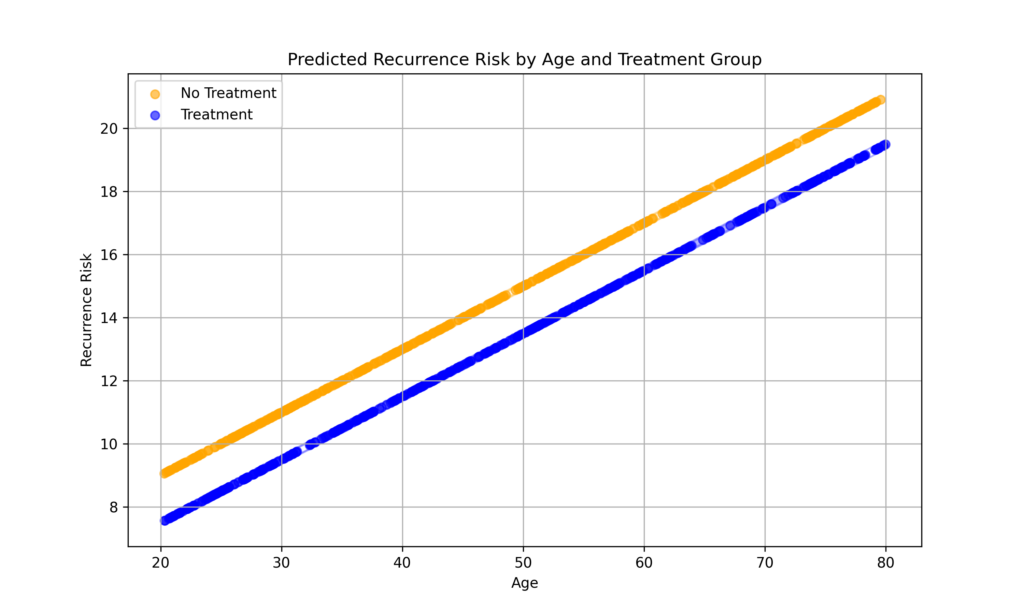
Example 2: Monte Carlo Simulation and Linear Regression
This example simulates the risk of recurrence using a linear regression model. The goal is to demonstrate how Monte Carlo simulation can be applied to assess the variability and confidence in predictions based on a linear regression model.
The risk of recurrence is evaluated using two independent variables: age (a continuous variable) and treatment status (a binary variable).
Required Python Libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
Step 1: define the parameters of simulation
np.random.seed(42) # Seed for reproducibility
num_patients = 1000 # Number of patients in the simulation
num_simulations = 1000 # Number of Monte Carlo iterations
# Parameters for the linear regression model
# True coefficients (for simulation purposes)
beta_0 = 5 # Intercept
beta_1 = 0.2 # Coefficient for age
beta_2 = -1.5 # Coefficient for treatment (binary: 0 or 1)
sigma = 2 # Standard deviation of the noise term
# Generate patient data
ages = np.random.uniform(20, 80, num_patients) # Ages uniformly distributed between 20 and 80
treatment = np.random.choice([0, 1], size=num_patients) # Random assignment to treatment groups (0 or 1)
Step 2: runs the regression model multiple time with generated data
predicted_risks = np.zeros((num_simulations, num_patients))
for sim in range(num_simulations):
# Generate recurrence risk with noise
noise = np.random.normal(0, sigma, num_patients)
true_risk = beta_0 + beta_1 * ages + beta_2 * treatment + noise
# Fit a linear regression model to the simulated data
# (For simplicity, we assume the same predictors for all simulations)
X = np.column_stack((np.ones(num_patients), ages, treatment)) # Design matrix
beta_hat = np.linalg.inv(X.T @ X) @ X.T @ true_risk # Ordinary Least Squares estimate
# Predict recurrence risk using the fitted model
predicted_risks[sim, :] = X @ beta_hat
Step 3 visualize the results with a plot of predicted risk against age for treatment and no treatment groups
plt.figure(figsize=(10, 6))
for treatment_group in [0, 1]:
group_mask = (treatment == treatment_group)
label = 'Treatment' if treatment_group == 1 else 'No Treatment'
color = 'blue' if treatment_group == 1 else 'orange'
plt.scatter(ages[group_mask], mean_risk[group_mask], alpha=0.6, label=label, color=color)
plt.fill_between(
ages[group_mask],
mean_risk[group_mask] - std_risk[group_mask],
mean_risk[group_mask] + std_risk[group_mask],
color=color, alpha=0.3
)
plt.title('Predicted Recurrence Risk by Age and Treatment Group')
plt.xlabel('Age')
plt.ylabel('Recurrence Risk')
plt.grid(True)
plt.legend()
plt.show()
Conclusion
Monte Carlo simulation is a powerful tool that enables modeling, analyzing, and optimizing clinical studies when faced with uncertainty. It provides a robust foundation for improving study design, supporting clinical and regulatory decisions, and predicting long-term outcomes. However, its effectiveness depends on the quality of underlying assumptions.


