When continuous variables can influence our analysis data, we can perform an analysis adjusted for these variables (covariates).
Consider treating hypertension with medication. In a standard ANOVA, we’d examine blood pressure values after one month of treatment (dependent variable) and whether the patient is in the treatment group or not (independent variable).
Similarly, we might analyze a class’s math results after six months of lessons.
In both cases, other variables can influence the results: initial blood pressure values in the first case and baseline math knowledge in the second.
These variables can significantly impact our analysis results. Ignoring them would be a mistake.
The ANCOVA test allows us to compare the effect of the independent variable on the dependent variable while accounting for the covariates.
The covariate is not the main variable of our study (such as hypertension therapy or mathematics teaching). Instead, it’s a continuous variable that can confuse our results if not considered. The ANCOVA test helps neutralize its effects.
ANCOVA works by first measuring the covariate’s influence on the final result and then removing this effect. After this adjustment, it compares the independent variable groups to detect significant differences in the outcome, now free from the covariate’s influence.
To perform ANCOVA, our data must meet several conditions:
- Linearity of the covariate with the dependent variable
- There must be a linear relationship between the covariate (e.g., pre-treatment blood pressure) and the dependent variable (e.g., blood pressure after 1 month of therapy). If this relationship isn’t linear, the results may be inaccurate.
- Independence of the covariate from the groups
- The groups should have similar levels of the covariate. For instance, if the treated group has significantly different pre-treatment blood pressure values than the untreated group, ANCOVA may fail to correct the result accurately.
- Homogeneity of regression slopes (one of the most crucial preconditions)
- The relationship between the covariate and the dependent variable must be consistent across groups. If the regression line’s slope differs between groups, ANCOVA shouldn’t be used.
- Normality of residuals
- Similar to ANOVA, the residuals—the difference between predicted and actual values—must have a normal distribution in ANCOVA, after accounting for the covariate’s effect.
- Homoscedasticity
- The variance of the dependent variable must be equal across all groups.
To perform ANCOVA using Python, we use the statsmodels library and specifically its ols() function, which stands for Ordinary Least Squares Regression. The ols() function is versatile, capable of handling various analyses including simple and multiple linear regressions, as well as ANOVA. The function’s behavior is determined by the arguments we provide. For ANCOVA, we use the following syntax:
model = statsmodels.ols('dependent_var ~ C(categorical_var) + continuous_covariate', data=df).fit()
This syntax specifies a dependent variable, an independent categorical variable (denoted by C), and a continuous covariate (added with +).
In this section, we present a comprehensive ANCOVA analysis, including assumption checks, using a fictitious clinical database. We examine a scenario where a group of individuals received hypertension treatment, comparing a new treatment to the standard one. Their baseline blood pressure serves as a covariate in this analysis.
First, let’s create our dataset:
import pandas as pd
import numpy as np
# Set a seed for reproducibility
np.random.seed(42)
# Generate a dataset
data = pd.DataFrame({
'Treatment': np.random.choice(['New', 'Standard'], size=100),
'Initial_Status': np.random.normal(120, 10, size=100),
'Final_BP': np.random.normal(130, 10, size=100)
})
# Adjust 'Final_BP' slightly based on 'Treatment' for demonstration purposes
data.loc[data['Treatment'] == 'New', 'Final_BP'] += 5
data.loc[data['Treatment'] == 'Standard', 'Final_BP'] -= 5
# Display the dataset
data.head()
Verifying the Assumption: Linearity Between the Covariate and Dependent Variable
import seaborn as sns
import matplotlib.pyplot as plt
# Scatter plot with a trendline
plt.figure(figsize=(8, 6))
sns.regplot(x='Initial_Status', y='Final_BP', data=data, scatter_kws={'s': 20}, line_kws={'color': 'red'})
plt.title('Initial Status vs Final Blood Pressure with Trendline')
plt.xlabel('Initial Status')
plt.ylabel('Final Blood Pressure')
plt.show()
Verifying the Assumption: Independence of the covariate from the groups
from scipy.stats import ttest_ind
# Test for independence
new_group = data[data['Treatment'] == 'New']['Initial_Status']
standard_group = data[data['Treatment'] == 'Standard']['Initial_Status']
t_stat, p_value = ttest_ind(new_group, standard_group)
print(f"T-statistic: {t_stat}, p-value: {p_value}")
The results: T-statistic: 0.8466418913639987, p-value: 0.399257484825168
Verifying the Assumption: Homogeneity of regression slopes
import statsmodels.formula.api as smf
# Add an interaction term
model_interaction = smf.ols('Final_BP ~ Initial_Status * Treatment', data=data).fit()
print(model_interaction.summary())
We can examine the interaction term (Initial_Status:Treatment). If it’s not statistically significant, the assumption of homogeneity of regression slopes holds. In this case, the result yields p = 0.212, supporting this assumption.
Verifying the Assumption: Normality of residuals
# Extract residuals from the model
residuals = model_interaction.resid
# Plot Q-Q plot for normality
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.figure(figsize=(6, 6))
stats.probplot(residuals, dist="norm", plot=plt)
plt.title("Q-Q Plot of Residuals")
plt.show()
The points on the Q-Q plot closely follow the diagonal line, confirming the normality of the residuals.
Verifying the Assumption: Homoscedasticity
from scipy.stats import levene
# Levene's test
stat, p_value = levene(data[data['Treatment'] == 'New']['Final_BP'],
data[data['Treatment'] == 'Standard']['Final_BP'])
print(f"Levene’s Test p-value: {p_value}")
Levene’s Test p-value: 0.5224243218854919
Conducting the ANCOVA Analysis
# Fit the ANCOVA model
model = smf.ols('Final_BP ~ C(Treatment) + Initial_Status', data=data).fit()
print(model.summary())
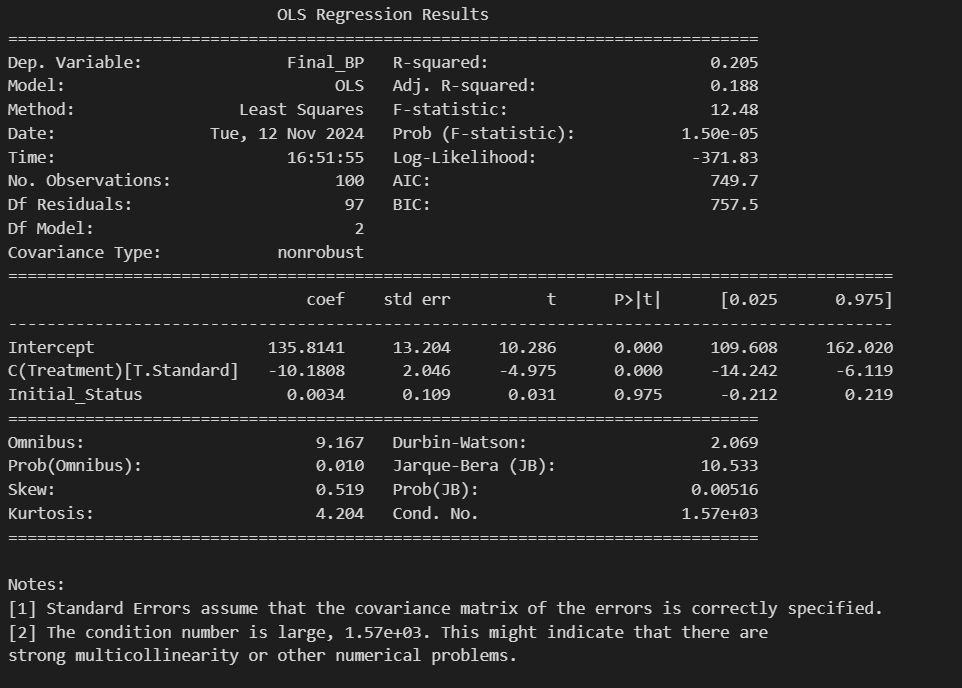
Results:
Let’s examine the results of the ANCOVA table:
- Intercept: The value of 135.8141 represents the mean post-treatment blood pressure when the initial state is zero. This isn’t particularly informative in this context, since blood pressure can’t actually be zero in reality.
- C(Treatment)[T.Standard]: This is a key result. The coefficient of -10.1808 indicates that the standard treatment is associated with a decrease in blood pressure of about 10.18 mmHg compared to the new treatment, after adjusting for the initial state. This effect is statistically significant (p < 0.001).
- Initial_Status: The coefficient of 0.0034 suggests a very weak relationship between the initial state and final blood pressure. However, with a p-value of 0.975, this effect is not statistically significant.
- R-squared: The value of 0.205 indicates that about 20.5% of the variance in final blood pressure is explained by the model. This suggests the model has moderate predictive capacity.
- F-statistic and Prob (F-statistic): The F-value of 12.48 with a very low p-value (1.50e-05) indicates that the model as a whole is statistically significant.
In summary, these results suggest that the standard treatment is significantly more effective in reducing blood pressure compared to the new treatment, even after controlling for the initial state. However, the model explains only a moderate portion of the variability in outcomes, indicating that there might be other important factors not considered in this analysis.


