Bayes’ Theorem

Understanding Probabilistic Reasoning

Bayesian statistics offers an alternative approach to probability and statistical inference, contrasting with the more widely used frequentist method. This comprehensive guide explores conditional probability, posterior probability, and statistical modeling through practical examples.

In the frequentist approach, event predictions are based on the number of observations. As more observations are made, both the event prediction and frequency estimation become more accurate.

In the Bayesian approach, predictions and frequency estimations are influenced by previously known conditions, incorporating prior probabilities and likelihood functions to update beliefs.

Let’s explore the difference between Bayesian and frequentist approaches through practical examples:

Medical Diagnosis Example:

• Frequentist approach: a doctor determines disease likelihood based solely on symptom frequency in past cases. For instance, if 80% of patients with chest pain had heartburn, they would predict heartburn 80% of the time.
• Bayesian approach: the doctor evaluates multiple factors including the patient’s age, medical history, and lifestyle, before making a diagnosis. For a young, athletic patient, they might assign a lower probability to heart problems despite similar symptoms.

Weather Prediction Example:

• Frequentist approach: predicting tomorrow’s rain probability based solely on historical rainfall patterns on similar days.
• Bayesian approach: combining historical weather data with current conditions like air pressure, wind patterns, and seasonal trends to make a prediction.

Used Car Purchase:

• Frequentist approach: when evaluating a used car’s likelihood of breaking down within a year, you would analyze historical records of identical cars (same age, mileage, and model) to determine the breakdown rate.
• Bayesian approach: while starting with the same historical data, a Bayesian would modify their prediction based on additional information. For instance, learning that the car was recently serviced would lower their estimated probability of breakdown.

Trying a Cooking Recipe:

• Frequentist approach: to evaluate if a new recipe is successful, you would need to prepare it multiple trials and gather feedback from many tasters. This repeated testing reveals how well the recipe performs.
• Bayesian approach: you begin by applying your cooking expertise to execute the recipe optimally. Then you refine the recipe based on taster feedback to improve the results.

Sports Betting

• Frequentist approach: to predict outcomes, one must analyze many historical games played by the same team against the same opponent, in the same stadium, with the same coach—a challenging task due to the rarity of identical conditions.
• Bayesian approach: first assess the team’s overall strength and likelihood of winning, then adjust predictions based on current factors like player injuries, field conditions, and other relevant circumstances.

Based on these examples, we can better define the frequentist and Bayesian approaches:

• The frequentist approach determines probability by repeating an experiment many times, establishing event likelihood as an objective measurement.
• The Bayesian approach begins with an initial belief that is continuously updated as new information becomes available, without requiring multiple experimental repetitions.

Bayes’ theorem can be expressed mathematically as follows:

P(A) – The prior probability: This is our initial belief about event A before we see any new data

P(B|A) – The likelihood: This represents the probability of observing the data B, given that A is true

P(A|B) – The posterior probability: This is what we’re solving for – the probability of A after we’ve observed B

P(B) – The marginal probability: The probability of observing event B regardless of whether A occurred

This theorem allows us to update our beliefs about hypotheses as we gather new evidence.

An example

Having explored the mathematical formula of Bayes’ theorem, let’s apply it to a real medical diagnostics scenario. This example demonstrates both the practical use of the formula and the critical role of Bayesian reasoning in clinical decision-making.

We’ll examine a common medical situation: assessing the reliability of a diagnostic test.

Consider a disease that has a 1% prevalence in the population. We need to diagnose whether a patient has this disease.

The base probability of having the disease is P(D+) = 0.01.

We have a diagnostic test with 95% sensitivity (it correctly identifies sick patients 95% of the time): P(T+|D+) = 0.95.

The test has 90% specificity—it correctly identifies healthy people 90% of the time. This means it incorrectly shows positive for 10% of healthy people: P(T+|D-) = 0.10

So the test can be positive in two scenarios: when testing sick patients (95% of the time) and when testing healthy patients (10% of the time).

To find the overall probability of a positive test result, we calculate:

(PT+) = P(T+|D+) P(D+) + P(T+|D-) P(D-)

Plugging in our numbers:

(PT+) = 0.95 * 0.01 + 0.10 *0.99

At first glance, a positive test result might seem to indicate a high likelihood of disease.

However, let’s apply Bayes’ theorem:

Surprisingly, even with a positive test result, the probability of having the disease is only 8.7%.

The seemingly counterintuitive result demonstrates why Bayes’ theorem is so important in medical diagnosis – even with a positive test result, the actual probability of having the disease is much lower than most people would expect, due to the low base rate of the disease in the population.

Bayes in Python: Implementation and Tools

Python provides a comprehensive ecosystem of libraries specifically designed for conducting Bayesian statistical analysis, making it an ideal platform for both beginners and advanced practitioners in Bayesian inference.

PyMC is the most widely adopted library in the Bayesian Python ecosystem. It offers robust capabilities for probabilistic programming and Markov Chain Monte Carlo (MCMC) sampling. Meanwhile, ArviZ, though not directly performing Bayesian inference, serves as an invaluable companion tool for sophisticated analysis, thorough diagnostic checking, and creating insightful visualizations of results generated by other Bayesian computation libraries.

PyMC’s greatest strength lies in its sophisticated yet user-friendly high-level abstraction layer. This design philosophy allows practitioners to focus on the statistical modeling aspects rather than computational details. Users can easily specify parameters, define probability distributions, and establish relationships between variables using intuitive syntax. The library then automatically handles the complex underlying calculations required for determining posterior probabilities, including implementing efficient sampling algorithms and convergence diagnostics.

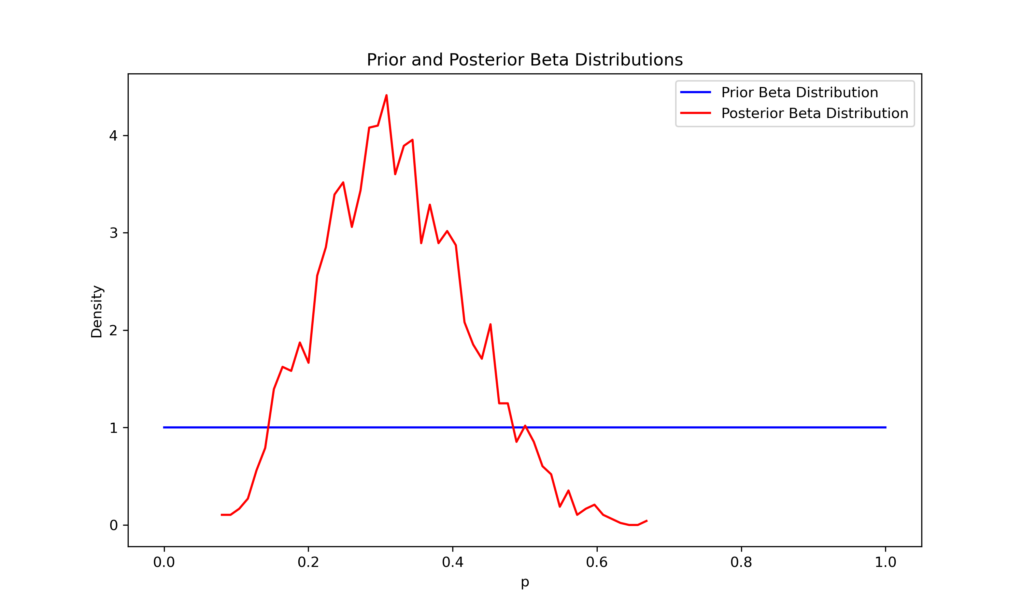
Consider a simple example using a binomial distribution, like flipping a coin where heads counts as success and tails as failure. Let’s say we observed 6 heads in 20 coin flips.

Our goal is to determine the posterior distribution for p—the probability of getting heads.

import pymc as pm
import arviz as az

k_observed = 6
n = 20

with pm.Model() as model:
    # Prior on p: Beta(1,1) is equivalent to a uniform distribution on [0,1]
    p = pm.Beta("p", alpha=1, beta=1)
    
    # Likelihood: Binomial with n=20 and probability p
    y = pm.Binomial("y", n=n, p=p, observed=k_observed)
    
    # Execute MCMC sampling
    trace = pm.sample(2000, tune=1000, chains=2, target_accept=0.95)
    
az.plot_trace(trace)
az.summary(trace)

The code begins by importing two essential libraries: PyMC (aliased as pm) for probabilistic programming and ArviZ (aliased as az) to visualize and analyze Bayesian models.

First, remember to install PyMC and ArviZ using the pip install command in your terminal.

The code defines two variables: k_observed (set to 6) and n (set to 20), representing the number of successful trials and total trials, respectively.

A probabilistic model is created using a context manager (with pm.Model() as model. Within this context, we specify the prior distribution for the probability of success p as a Beta distribution with parameters alpha=1 and beta=1. This Beta(1,1) distribution is equivalent to a uniform distribution over [0,1], meaning it assigns equal probability to all possible values of p.

Next, we define the likelihood of the observed data using a Binomial distribution. The distribution is parameterized by the total number of trials n and the probability of success p. We link this to our data by passing k_observed to the observed pm argument. Binomial, which represents our observed number of successes.

The MCMC sampling is then performed using the pm.sample function. The function is configured to draw 2000 samples from the posterior distribution, with an additional 1000 tuning steps to allow the sampler to adapt. Two chains are run in parallel, and the target_accept parameter is set to 0.95 to control the acceptance rate of the sampler.

Finally, the trace of the sampled values is visualized using az.plot_trace(trace), which generates trace plots for each parameter in the model. Additionally, a summary of the trace is printed using az.summary(trace), providing statistical summaries such as the mean, standard deviation, and credible intervals for the parameters.

Let’s explore what each parameter means in the results of a Bayesian analysis using PyMC and arviz:

• mean: The average value of the posterior distribution samples, representing our best estimate of the parameter.
• sd: The standard deviation of the posterior distribution samples, showing how much the values vary from the mean.
• hdi_3% and hdi_97%: The Highest Density Intervals, showing the range containing 94% of the posterior distribution’s most probable values. These are similar to confidence intervals but specific to posterior distributions.
• mcse_mean: The Monte Carlo standard error of the mean, indicating how much uncertainty our sampling method introduces into the mean estimate.
• mcse_sd: The Monte Carlo standard error of the standard deviation, showing how much uncertainty our sampling method introduces into the variance estimate.
• ess_bulk: The Effective Sample Size for the main part of the distribution, telling us how many truly independent samples we have in the central region.
• ess_tail: The Effective Sample Size for the distribution’s edges, telling us how many truly independent samples we have in the tail regions.
• r_hat: The Gelman-Rubin convergence metric. A value near 1 shows that our sampling has successfully converged.

Together, these parameters help us assess both the results of our analysis and how well our sampling method performed.

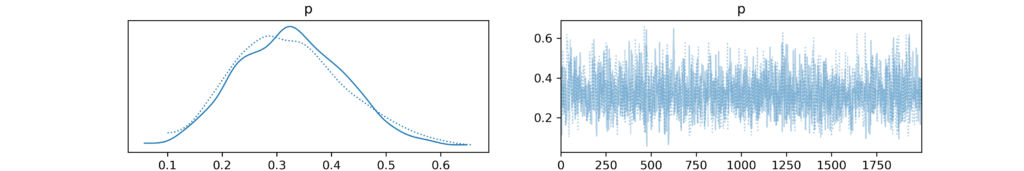
The az.plot_trace(trace) function creates two key visualizations for each model parameter:

1. Trace Plot: Shows how parameter values change across MCMC sampling iterations. A well-mixed pattern without clear trends indicates good sampling convergence.
2. Posterior Distribution Plot: Displays the estimated posterior distribution, showing the most probable parameter values through a density plot of the samples.

In conclusion, PyMC stands out as a versatile and powerful tool for Bayesian inference in Python. It effectively connects Bayesian theory with practical applications, enabling users to analyze real data with ease while providing flexibility, computational efficiency, and seamless integration with Python’s scientific ecosystem.